●対策をする際は、[1日1テーマ]と決めて進めると、効率よく計算力・スピード・正確性を身につけることができる。
●本番形式の練習や苦手の克服を取り入れることで、試験対策としての完成度が高まる。
[四則逆算]とは、[足し算・引き算・かけ算・わり算]といった四則演算のルールをもとに、空欄に入る数値を逆算して求める問題形式のことを指します。制限時間内に正確な答えを導くには、問題を解くためのコツや効率的なアプローチを知っておくことが大切です。
この記事では、[四則逆算の基本ルール]から[よく出る問題パターン]、さらには[スピードアップに繋がる時短テクニック]までを丁寧に解説しています。是非最後まで読んで、効率よく対策を進めてくださいね。
四則逆算とは

四則逆算とは、[足し算・引き算・かけ算・わり算]といった四則演算のルールをもとに、空欄に入る数値を逆算して求める問題形式です。SPIや適性検査では、[□+7=12]のような問題が出題され、そこから[□=5]といった元の数を導き出す力が問われます。
一見シンプルですが、複数の演算が組み合わさっていたり、計算手順を誤ったりするとミスにつながりやすいため、基本ルールの理解に加えて、正確かつ素早い計算力が求められます。
四則計算の問題数と制限時間
SPIなどの適性検査では、10〜15問ほど出題され、制限時間は5〜10分程度に設定されていることが一般的です。例えばSPIテストセンターの[非言語分野]では、四則逆算のような計算問題が時間制限付きで出題されるため、正確さとスピードの両立が求められます。
時間に余裕がない中で焦ってしまうとケアレスミスが起きやすいため、計算パターンに慣れておくことが得点アップにつながります。
四則演算が含まれる主な試験
四則逆算を含む四則演算問題は、以下のような試験で出題されることが多いです。
- SPI(テストセンター・Webテスティング形式)
- 玉手箱(主に非言語の計算問題)
- CAB
- 公務員試験(教養試験)
- 企業独自の適性検査・筆記試験
いずれの試験でも、[基本的な四則演算力=思考の土台]として重視されています。特に事務系・営業系・コンサル系職種を希望する場合には、数的処理がスムーズにできることをアピールする意味でも重要です。
超基本!四則演算の基本的な法則

四則逆算をスムーズに解くには、まず四則演算の基本的なルール(法則)を押さえておく必要があります。ここでは、よく出題される3つの基本法則を紹介します。
※本項では、計算の基礎力を高めるために[四則演算に共通する3つの基本法則(交換・結合・分配)]を紹介しています。
一部のサイトではこれらを[四則逆算で活用される法則]として紹介しているケースもありますが、これらは“逆算のためのテクニック”とは異なり、四則演算の計算ルール(性質)です。
実際の逆算問題では、別途[式を逆からたどる思考法]や[操作の逆(加→減、掛→割)]を使うことが必要です。
①交換の法則
足し算と掛け算では、順序を入れ替えても答えは変わりません。
- 2+3=3+2(答えは5)
- 4×5=5×4(答えは20)
このように[A+B=B+A][A×B=B×A]が成り立つことを交換の法則といいます。引き算や割り算ではこの法則は成り立ちません。
②結合の法則
足し算・掛け算では、計算する順番を変えても答えは同じです。
- (2+3)+4=2+(3+4)=9
- (2×3)×4=2×(3×4)=24
このように、カッコの位置を変えても結果が変わらない法則を結合の法則といいます。こちらも、引き算・割り算では成り立たないため注意が必要です。
③分配の法則
掛け算は、足し算・引き算に[分配]して適用できます。
- 2×(3+4)=2×3+2×4=6+8=14
- 5×(6−2)=5×6−5×2=30−10=20
このように、掛け算がカッコの中のそれぞれの項に分配されることを分配の法則といいます。式を展開したり整理したりする場面で非常に便利な法則です。
逆算問題を解くために覚えておきたい実践的な解き方・テクニック

SPIなどの試験で出題される[四則逆算]では、与えられた計算式から“もとの数”を導き出す力が求められます。ただ速く計算するだけではなく、どこから手をつけるか、どの順番で考えるかが大切なポイントです。
ここでは、逆算問題を解くために覚えておきたい3つの基本テクニックを紹介します。
①引き算で元の数を求める
逆算問題を解く上で必ず押さえておきたいのは、足し算の答え(和)と一方の数が分かっている場合、もう一方の数は引き算で求められるという基本的な考え方です。
これは、合計と一方の数から、未知の数(例えば、式の中で□で示される数)を特定する計算方法の1つです。
Q:□に入る数字はなんですか?
□ + 7 = 12
● ステップ①:問題を読み取る
[ある数(□)に7を足したら12になった]と書かれています。
● ステップ②:[足し算]だとわかる
式の中に[+]があるので、これは足し算の問題ですね。
● ステップ③:[足し算の逆=引き算]で考える
足し算は、[逆にたどると引き算になる]というルールがあります。
[12から7を引いたら、もとの数が出る]と考えましょう。
● ステップ④:実際に計算する
12 − 7 = 5
なので、□ に入る答えは 5 です。

学生
なぜ[引き算]で元の数が出るの?

アドバイザー
例えば、こう考えてみてください。
もし[5 + 7 = 12]だったら、5が□に入るはずです。
つまり、逆に[12 − 7]で考えると、もともとの[5]がわかるということです。
計算の順番を逆にしないように気をつけてください。
▼NG例
[7 − 12]など、引く順番を逆にしないようにしましょう。
必ず、[全体の合計(=答え)]から[わかっている数字]を引く、という流れです。
練習問題
答え
②割り算で元の数を求める
逆算問題では、掛け算で作られた式からもとの数を割り算で求めることがあります。
これも四則逆算ではとてもよく出る基本のパターンです。
Q. □に入る数字は何ですか?
□ × 4 = 28
●ステップ①:[掛け算]でできた式だと読み取る
[□を4倍したら28になった]と考えましょう。
● ステップ②:[掛け算の逆=割り算]で解く
掛け算の逆は割り算です。つまり[28 ÷ 4]で答えが出ます。
● ステップ③:計算する
28 ÷ 4 = 7
→ 答えは 7

学生
なぜ[割り算]なの?

アドバイザー
[ある数を4倍したら28になった]ということは、[28を4で割れば、元の“ある数”がわかる]ということです。これは、逆にたどる=逆算という考え方です。
割り算の順番を間違えないようにしてください。
例えばこの問題で[4 ÷ 28]としてしまうと、不正解です。
練習問題
答え
③計算の逆順を意識する
逆算の中でも少しレベルが上がるのが、2つ以上の計算が含まれた問題です。
この場合は、計算された順番とは逆の順番で戻るという考え方が大事です。
Q. どの数に3をかけて、さらに4を足すと19になりますか?
(□ × 3)+ 4 = 19
●ステップ①:[最後に何をしたか]を見る
最後に行ったのは[+4(4を足す)]です。
● ステップ②:[逆にたどる]ために、まず4を引く
19 − 4 = 15
→ これで[□ × 3 = 15]になります。
● ステップ③:さらに掛け算の逆(割り算)で戻す
15 ÷ 3 = 5
つまり、答えは 5となります。
(5 × 3)+ 4 = 15 + 4 = 19 で確認もバッチリです。

学生
このようなときに覚えるべきルールやコツなどはありますか?

アドバイザー
「足された数 → 引く」や「掛けられる数 → 割る」のように、やったことの逆を、逆の順番でたどるのがコツです!
練習問題
答え
これだけは覚えたい!四則逆算の基本の解き方

四則逆算で難しそうに見える問題も、3つの基本ルールさえ覚えておけば、落ち着いて解けるようになります。ここでは、四則逆算で最低限覚えておきたい基本の解き方を3つ紹介します。
四則演算の「逆操作」を覚える
四則演算とは、足し算(+)・引き算(−)・かけ算(×)・わり算(÷)の4つの計算のことです。逆算では、この[計算の逆=逆操作]を理解しておくことがとても大事です。
| 元の計算 | 逆算で使う操作(逆操作) |
|---|---|
| 足し算(+) | 引き算(−) |
| 引き算(−) | 足し算(+) |
| かけ算(×) | わり算(÷) |
| わり算(÷) | かけ算(×) |
- □ + 6 = 10 → 10 − 6 = 4
- □ × 5 = 30 → 30 ÷ 5 = 6
このように、[何をされたか?]を逆にたどることで、もとの数が求められます。
式の中のカッコは最初に処理する
逆算に限らず、計算問題でカッコ( )があるときは、必ずそこから計算(または逆算)します。カッコは[この中を先にやってね]というサインです。
- (□ + 3) × 2 = 14
→ まず[×2]を逆操作で[÷2] - 14 ÷ 2 = 7
→ 次に[□ + 3 = 7]を逆操作で[−3] - 7 − 3 = 4
→ よって、答えは 4
カッコがあると少しややこしく見えるかもしれませんが、[中を最初に処理する]→[逆にたどる]という流れを守れば解けます。
計算の順序は「×・÷」→「+・−」でおこなう
複数の計算が並んでいるときは、計算の優先順位(ルール)を守ることが大切です。
これは[計算のきまり]として決まっていて、以下の順番で進めます。
- カッコがある場合は 最初にカッコの中を計算
- 次に、かけ算(×)・わり算(÷)を先に計算
- 最後に、足し算(+)・引き算(−)を計算
- □ × 3 + 6 = 21
→ まず「+6」の逆操作で「−6」 - 21 − 6 = 15
→ 次に「□ × 3 = 15」の逆操作で「÷3」 - 15 ÷ 3 = 5
このように、計算の順序に注意しながら、逆の順番でたどることが逆算ではとても大切です。慣れるまではメモを取りながら、1ステップずつ解く習慣をつけることをオススメします。
四則逆算の代表的な問題パターン8選

四則逆算の問題は、大きく分けて[単発の逆算]と[2段階以上の複合逆算]に分かれます。ここでは、SPIなどでよく出る代表的な8パターンを紹介します。それぞれの問題の考え方と逆算のポイントを押さえて、得点アップに繋げましょう。
①【足し算の逆】合計から一方の数を求める問題
【問題例】
□ + 6 = 15
解き方

ポイント
②【引き算の逆】差と片方からもう一方を求める問題
【問題例】
□ − 8 = 5
解き方

ポイント
③【かけ算の逆】積から一方の数を求める問題
【問題例】
□ × 4 = 36
解き方
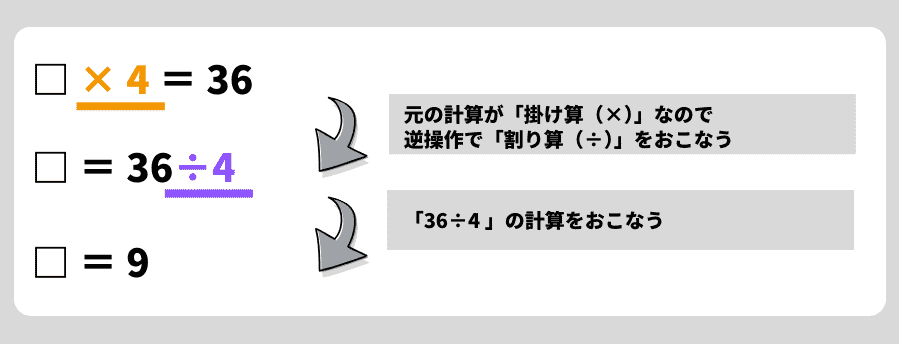
ポイント
④【割り算の逆】商と一方からもう一方を求める問題
【問題例】
□ ÷ 3 = 7
解き方
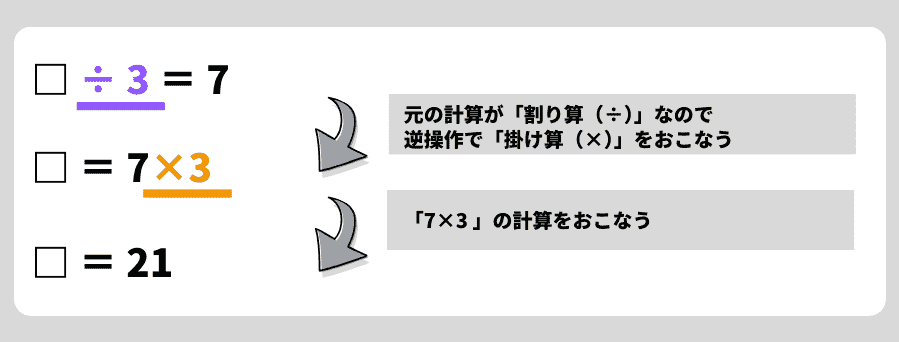
ポイント
⑤【2段階計算①】かけ算とたし算を逆にたどる問題
【問題例】
(□ × 2)+ 5 = 21
解き方

ポイント
⑥【2段階計算②】たし算とその後のかけ算を逆にたどる問題
【問題例】
(□ + 4)× 3 = 27
解き方
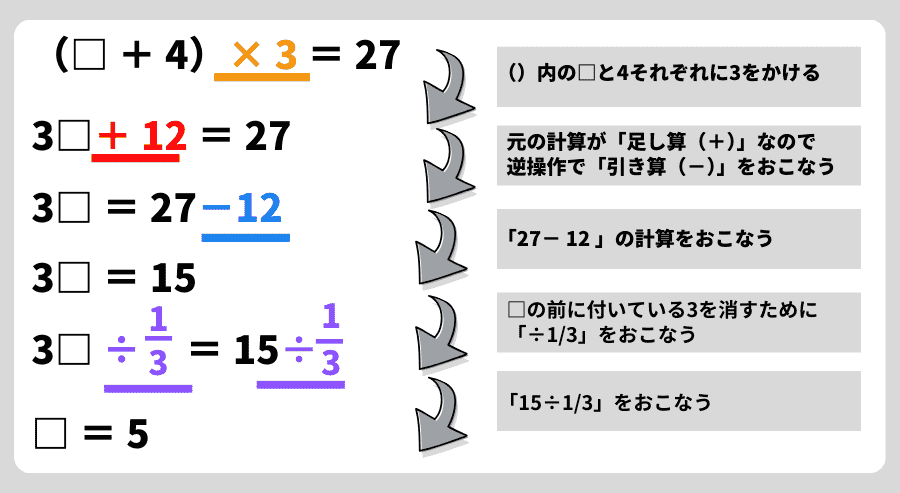
ポイント
⑦【カッコあり】計算の順番に注意して逆算する問題
【問題例】
(□ − 2) × 4 = 32
解き方
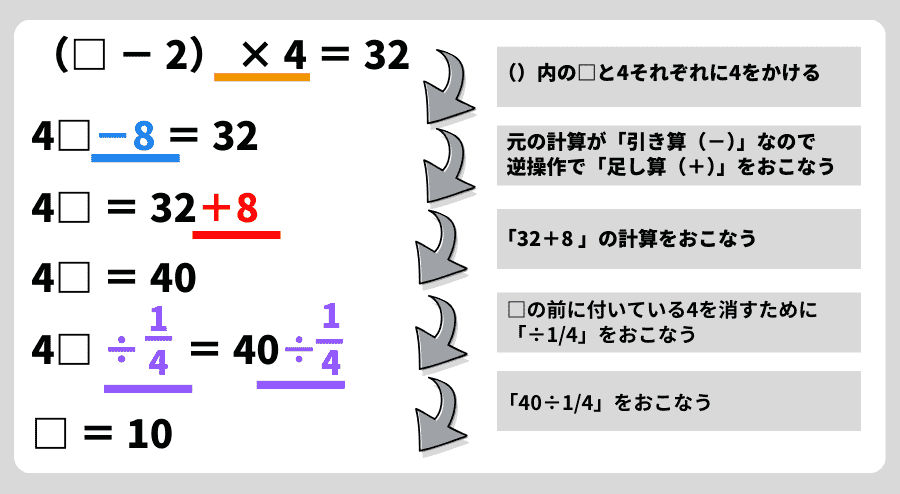
ポイント
⑧【両辺に変数】方程式のような形を逆算する問題
【問題例】
2 × □ + 3 = □ + 11
解き方

ポイント
正解率がグッと上がる!四則逆算の解き方ポイント

四則逆算では[計算力]だけでなく、[式の整理の仕方]や[ちょっとした工夫]が正解率を大きく左右します。ここでは、解き方がスムーズになり、ミスも減らせるポイントをご紹介します。
逆算しやすくするために「□=」の形に整える
問題文にそのまま出てくる式は、右側に□があることもあれば、左側に□がある場合もあります。どちらでも解けますが、基本は[□=]の形に揃えて考えると整理しやすくなります。
8+□=13
→ □=13−8
→ 答え:5
このように、□の位置を左側に持ってくることで、何をすれば答えが出るかがより明確になります。
小数と分数はどちらかに揃えて計算する
1つの式に小数と分数が混ざっていると、計算ミスの原因になります。そこで、小数なら全て小数、分数なら全て分数に揃えてから計算するのがオススメです。
0.5+1/4
→ 分数に統一
→ 1/2+1/4=2/4+1/4=3/4
自分が得意な方に揃えると、計算ミスなく進めやすくなります。
分数が複数あるときは分母を合わせる
分数同士の計算では、[分母を共通にする=通分(つうぶん)]が必須です。通分しておかないと、たし算や引き算が正確にできません。
1/3+1/6
→ 分母を6に揃える
→ 2/6+1/6=3/6=1/2
通分は手間に見えて、むしろミスを減らす近道です。
わり算は「分数」に変えて計算するとラクになる
わり算が含まれる式を解くときは、÷の形を分数に変えると、計算がスムーズになります。
6 ÷ 3
→ 6 × (1/3)
→ 2
[割る数を“ひっくり返してかける”]というルールを使えば、複雑な式も一気に解きやすくなります。特に小数の割り算では、この考え方がとても有効です。
式をそのまま書き出して整理する
頭の中で全部解こうとせず、式を紙に書き出すことが何より大切です。複雑な問題ほど、途中式が見えることで「どこで間違えたか」がわかりやすくなります。
(□+2)×3=18
→ 式を順に整理:18÷3=6 → 6−2=4
[見える化]するだけで、スッと理解することができます。
計算後は「検算」で答え合わせをする
答えが出たら、[元の式に戻して本当に正しいかをチェックする=検算(けんざん)]をしましょう。これでケアレスミスを防ぎ、正答率をさらにアップさせることができます。
答えが4のとき
→ (4+2)×3=18?
→ 6×3=18
→ OK!
時間が許す限り、答えの再確認をしましょう。
時間切れを防ぐ!四則逆算を早く解くためのコツ

四則逆算でスピードと正確さを両立させるには、事前の準備と当日の解き方がとても重要です。ここでは、早く解くためのコツを紹介します。
よく出る逆算パターンを事前に覚えておく
四則逆算の問題には、頻出のパターンがあります。例えば[□+〇=△][(□×〇)+△=◇][分数を使った逆算]など、よく出る型が決まっているため、あらかじめ覚えておくことで、解答にかかる時間を大幅に短縮できます。
- □×4+2=18
→ 4□=18-2
→ 4□=16
→ □=16÷4
→ □=4 - (□+3)×2=12
→ 2□+6=12
→ 2□=12−6
→ 2□=6
→ 2□÷2=6÷2
→ □=3
本番を意識して“時間ありき”で練習する
普段の練習で時間を意識しないクセがついていると、本番で時間配分に失敗するリスクが高まります。そこで、日頃から本番と同じ制限時間を設定して問題を解く習慣をつけることが重要です。
- 10問を5分以内に解く
- 1問あたり30秒以内を目安にする
- タイマーを使って本番環境をシミュレーションする
制限時間を意識して繰り返すことで、時間感覚が自然と身につきます。
選択肢を先に見るクセをつける
逆算問題では、問題文よりも選択肢を先に見ることで[何を問われているか ] が明確になる場合があります。とくに似たような選択肢が並んでいるときは、[違い]を先に見つけることで、注目すべきポイントが絞り込めます。
- 選択肢に共通点がある場合、その部分の詳細な確認は省略する
- 全文を読む前に、選択肢をヒントに[この数値を求めれば良い]といった逆算の糸口を探る
わからない問題は思い切って飛ばす
1つの問題にこだわって時間をかけすぎてしまうと、他の問題にかける時間がなくなってしまう可能性があります。少し考えてもわからない場合は、「後でもう1回考えよう」と割り切り、次の問題に取り掛かりましょう。
- 30秒以上悩む問題は、一旦飛ばす
- 残り時間が5分を切ったら、残りの中で確実に解けるものに集中する
同じミスを繰り返さないよう「間違いノート」を作る
同じような問題で何度も間違えてしまうと、正答率は安定せず得点アップも期待できません。特に逆算問題では、ミスの原因を特定し対策しなければ、同じ間違いを繰り返してしまう可能性があります。
そこでおすすめしたいのが、間違えた問題や苦手なポイントを記録する[間違いノート]の作成です。なぜ間違えたのか、どの計算過程でつまずいたのかを具体的に書き残すことで、類似問題への対応力が格段に向上します。
間違いノートを活用して弱点を克服し、正答率を高めれば、一度理解した問題や似た形式の問題は、より迅速かつ正確に解答できるようになるでしょう。その結果、試験全体の時間配分に余裕が生まれ、他の問題にも落ち着いて取り組めるようになります。
焦らず正確に解く力を養うためにも、ぜひオリジナルの間違いノートを作ってみてください。
- ミスの原因(計算ミス/順序の取り違え/見落とし)
- 正しい解き方
- 自分が引っかかりやすいポイント(例:分数、カッコ、順番)
この習慣が、短期間での解き直し力と判断力の向上に繋がります。
1週間で実力アップ!四則逆算の学習プラン

四則逆算はSPIや適性検査で頻出の分野ですが、何となくで取り組むと時間ばかりかかってしまいます。そこでオススメなのが、7日間で[基礎→応用→本番形式]をしっかりおさえる学習プランです。
短期間でも集中して取り組めば、計算力・パターン把握力・時間感覚の全てを一気に引き上げることができるでしょう。
【1日目】四則逆算の基礎を理解する
初日は、「逆算とは何か?」を正しく理解することから始めてください。足し算・引き算・かけ算・わり算、それぞれにどんな逆操作が必要かを覚えましょう。
- 四則演算の逆を確認する
- [たし算・ひき算]だけで解けるような、やさしい逆算問題から取り組む
- [□+6=13]→[13−6=□]の感覚をつかむ
【2日目】よく出る定番パターンを攻略する
2日目は、SPIでよく出る定番の逆算問題を反復練習します。型に慣れることで、解くスピードと正解率が一気に上がります。
- 単発の逆算(加減・乗除)15問を解く
- 2段階計算(例:□×2+4=20)15問を解く
- どの順で解くか、逆順の考え方に慣れる
【3日目】計算の順序とカッコの扱いに慣れる
3日目は、複数の演算が含まれる式やカッコ付きの問題に取り組みましょう。計算の順番を間違えないよう、先にどこから計算すべきなのかを意識して解いてみてください。
- カッコのある問題(例:(□+2)×3=18)30問を解く
- [×÷を先に、カッコは最初]などのルールを整理する
- 間違えた問題は式を書き出して丁寧に分析する
【4日目】弱点を洗い出し、苦手パターンに集中する
4日目は、これまでに解いた問題を見返して自分の苦手なパターンを明確にします。[分数が出ると詰まる ] [順序がごちゃごちゃになる ] など、課題を洗い出し、重点的に対策していきましょう。
- 間違えた問題をノートにまとめ直す
- 分数・カッコ・2段階など、苦手な型を重点的に練習する
- 成長が見えるように正答率を記録する
【5日目】単発・複合・カッコ付きの問題をランダムで解く
5日目は、実践に近い形で様々なタイプの問題を混ぜて解いていきます。解く順番を間違えないよう注意しながら、一問ずつ逆順でたどる力を試しましょう。
- 出題形式を混ぜた練習問題(30問)を解く
- 制限時間15分でトライする
- 解いたあとは必ず検算(確認)する
【6日目】試験本番と同じ環境で解く
6日目は、試験本番を意識したシミュレーションをおこないましょう。時間・問題数・緊張感を再現し、集中できる環境で取り組んでください。必ず時間を測りながら実施し、本番に向けた準備を整えましょう。
- 模擬テスト(例:20問/10分)を1セットで解く
- できれば同じ時間帯で解く
- 解けなかった問題はすぐに復習する
【7日目】最終チェック&総仕上げをおこなう
7日目は、これまでの学習内容を総まとめする日です。解けなかった問題の見直しと、自信を持って解けた問題の確認をおこなって、最終調整をしましょう。
- 1日目〜6日目の復習(特にミスが多かった問題)をする
- 逆算のポイントや解き方の流れをノートで整理する
まとめ
四則逆算は、SPIなどの適性検査で頻出する重要な問題形式です。1つひとつの計算はシンプルでも、限られた時間内で正確に解くにはコツと慣れが必要です。
本記事で紹介したように、「逆操作の理解」「パターンごとの対策」「時間を意識した練習」「苦手分野の洗い出し」などを意識して取り組めば、短期間でも得点を伸ばすことが可能です。
是非今回の学習法を参考にして、四則逆算の苦手を克服し、適性検査での高得点を目指しましょう。
四則逆算だけで満足していない?面接対策もエージェントと一緒に効率よく進めよう
「就職エージェントneo」は業界のパイオニアとして最も歴史がある就活エージェントです。東証プライム上場企業や大手グループの求人から中小・ベンチャー企業の求人を保有しており、累計紹介企業数10,000社、内定支援実績45,000件を誇ります。
10年後を見据えた企業探しや面接後の個別フィードバックなどをおこなっており、Googleの口コミ評価は4.5と高水準です。
その他、いきなり責任者面接を受けられる特別推薦枠や、書類選考・一次選考が免除になる求人の取り扱いもあることから、時期によっては最速1日で内定が出る場合もあります。
就職エージェントneoのサービスは、就活生1人ひとりに専任のアドバイザーが付き、就活相談や選考対策などもおこなっているため、就活出遅れ組の学生にもオススメのサービスです。
「1人で自己分析をやってみたけど合っているのかわからない…」「自己分析のやり方を調べてもピンとこない…」といった就活生は、是非一度私たちにご相談ください。




